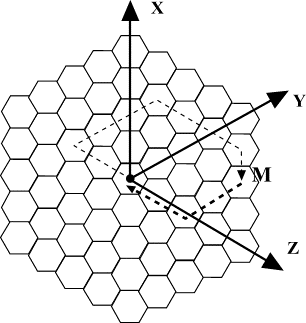An attempt was made to count all the cranberries in the swamps located in the surroundings of Rybinsk. It appeared convenient to split the surface of the swamp into regular hexagonal cells. One of these cells was considered as the central one, where the helicopter hovered. Three directions were marked (see picture).

After that a hired student landed in the central cell and wandered around for a certain time. He counted the berries and recorded his movements as he walked. Movements were recorded as a sequence of transitions from one cell to another through their common side along one of the marked (or reverse) directions. The route consisted of linear sections determined by directions (X, Y, or Z) and lengths (signed nonzero integers). A movement in the marked direction is represented with positive numbers, in the reverse direction — with negative numbers.

Your task is to write a program, which determines a route from the last cell visited by the student back to the central cell, having the least possible number of cells in it.

The first line of the input contains n — the length of the route (n > 0). Each of the following n lines contains a letter denoting a direction (X, Y, or Z) and a signed integer l (l ≠ 0) denoting the length of the section (in cells). The letter and the number are separated by one space.

While wandering, the student moved away from the central cell for no more than 100 cells in each of marked and reverse directions. The total length of the route does not exceed 32000 linear sections.

The output must contain the description of a route from the last cell visited by the student back to the central cell, having the least possible number of cells in it.

The first line of the output must contain m — the length of the route (number of sections in the back route, m ≥ 0). The following m lines of the output must contain the description of the sections of the back route in the same format as in the input.