| ENG RUS | Timus Online Judge |
2200. He is not a knight for you 2Time limit: 4.0 second Memory limit: 256 MB Igor is a chess player. After another training session, Igor and his partner decided to play with only one knight, but using not one chessboard, but several at once. Recall that the knight moves in an “L” shape in all directions, moving 2 squares along one axis and 1 square along the other. All possible moves for a chess knight are illustrated in the figure: 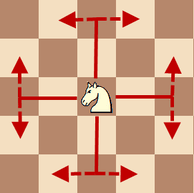 On a rectangular table marked with a square grid, Igor laid out N boards, each of which is a rectangle of at least 3 × 3 (at least 3 squares along each axis). The boards are arranged so that their sides are parallel to the sides of the table, and the corners of the boards are strictly at the nodes of the square grid. Moreover, no two boards touch each other, neither by sides nor even by corners. The center of the table is chosen as the origin, and the coordinates do not exceed M in absolute value. In a certain cell of one of these N boards, Igor placed the knight. You need to count how many boards the knight can visit by sequentially making its moves. The knight can only move on one board, as well as between them if it can do so in one move. It is allowed to visit previously traversed cells and boards. InputThe first line contains two integers N and M (1 ≤ N ≤ 5 · 104, 2 ≤ M ≤ 109) separated by a space. The second line contains two integers x and y — the coordinates of the lower left corner of the cell where the knight is located (−M ≤ x, y < M). In each of the following N lines, four integers are given separated by spaces: xLi, yLi, xRi, yRi, which define the next chessboard, where (xLi; yLi) are the coordinates of the lower left corner of the board, and (xRi; yRi) is the upper right corner (−M ≤ xLi < xRi ≤ M, −M ≤ yLi < yRi ≤ M). It is guaranteed that the size of the board in each dimension is at least 3, that is, xRi − xLi ≥ 3 and yRi − yLi ≥ 3, and that no two boards touch each other, neither by sides nor even by corners. It is guaranteed that the cell with the knight will be located on some board, that is, for some i, xLi ≤ x < xRi and yLi ≤ y < yRi. OutputIn a single line, output one integer — the number of boards that the knight can visit, including the board from which it starts its journey. Samples
NotesIllustration for the first example: 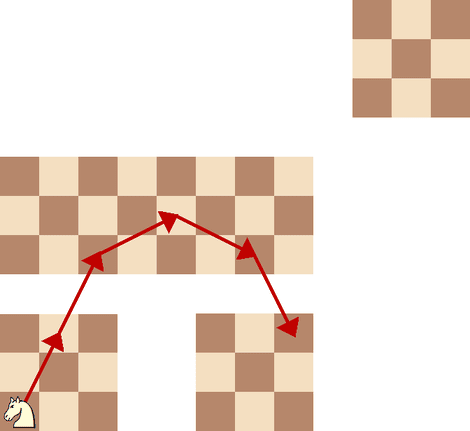 Problem Author: Vadim Barinov Problem Source: University academic school olympiad in informatics 2020 Tags: graph theory |
