| ENG RUS | Timus Online Judge |
2191. Piecewise Linear FunctionsTime limit: 3.0 second Memory limit: 256 MB Vadim is a big fan of piecewise linear functions. They have their limitations, and not every function can be represented as piecewise linear. Vadim will gladly tell you what they are. A function is called piecewise linear if its graph can be represented as a polyline with N vertices. Specifically, it is defined by n pairs of numbers (x1, y1), (x2, y2), …, (xN, yN), which are the coordinates of the vertices of the polyline. The condition must hold that
This set of points defines a function of one argument, whose value at xi is yi, and on the intervals between these points, it is linear. The domain of such a function is the segment [x1, xN]. Valya invented his own class of functions with one variable, which he called modular. A modular function consists of N terms, each of which has one of two forms: |ai · x + bi| or −|ai · x + bi|. Here, x is the variable, and ai and bi are the parameters of the function, while | … | denotes the absolute value. Thus, a modular function with N terms has the form
Vadim wanted to check whether modular functions are not worse than his favorite piecewise linear ones. He brought a piecewise linear function with N vertices. Now try to find a modular function with exactly N terms that is identically equal to the given piecewise linear function on the segment [x1, xN]. InputThe first line contains an integer N — the number of vertices of the polyline (2 ≤ N ≤ 105). Next, there are n lines, each containing two integers xi, yi — the coordinates of the next vertex (−105 ≤ xi, yi ≤ 105). It is guaranteed that the coordinates xi are strictly increasing, that is,
OutputOutput a single line containing the modular function with exactly N terms that is identically equal to the given piecewise linear function on the segment [x1, xN]. Follow the format shown in the examples. The function should consist of N terms |ai x + bi|, separated by the signs + and - (codes 43 and 45). It is allowed to place a leading minus before the first term. Each term must be enclosed in two symbols | (code 124). Inside the term, there must be a sign + (or -, if bi is negative). The left operand consists of a real number ai and the variable x (code 120); the multiplication sign between them does not need to be written, it is implied. It is not allowed to omit ai or bi, even if ai = 1 or bi = 0; the left operand cannot be omitted if ai = 0.There must be exactly N such terms. It is allowed to use terms that are identically equal to zero. They can be written as |0x+0|.The size of the output file must not exceed 8 MB. The answer is considered correct if at any point in the segment [x1, xN], the value of your modular function differs from the value of the given piecewise linear function by no more than 0.01. Samples
NotesIllustration for the third example: 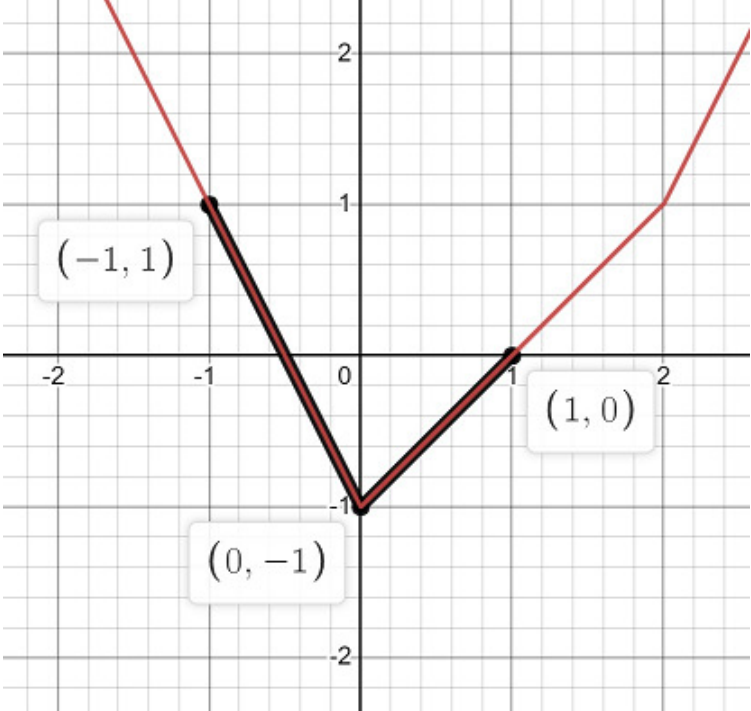 Problem Author: Valentin Zuev, Vadim Barinov Problem Source: Ural Regional Contest Qualifier 2022 Tags: mathematics |
