| ENG RUS | Timus Online Judge |
1623. Fractal LabyrinthTime limit: 1.0 second Memory limit: 64 MB Roman adores all kinds of labyrinths. He solves them since his early childhood.
Yesterday he found a new, extremely amazing sort of labyrinth. He called it a "fractal labyrinth".
Imagine a house with N doors. Inside it, there are K houses, each of them an entire copy of the "outer" one. Some doors are connected by roads. If you draw these roads, you get something like this: 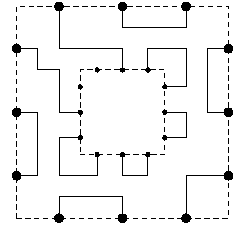 Remembering that each "inner" house is a copy of the "outer house", you get the following picture
as a result: 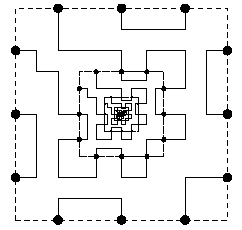 The following picture is an example of a house with 2 inner houses: 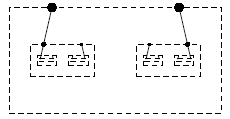 For outer house, some door is defined as "input" and some door as "output", so we finally come up to a labyrinth. Assuming that length of each road is 1, find the length of the shortest path in such labyrinth. InputIn the first line there are numbers N Each road description is formatted in the following way: <house-number>.<door-number> - <house-number>.<door-number> where left and right part of description specify the connected doors (a door is described by its number and
number of house it belongs to). Each road is bidirectional. The "outer" house has number 0, "inner" houses have numbers from 1 to K. Door numbers start with 0. No two roads connect the same pair of doors. No road connects a door to itself. In the last line there are numbers of input and output door Di and Do. These numbers may coincide. OutputIf there exists a path from input to output, print the minimal length of such path. Otherwise, print "no solution". Samples
Problem Source: SPbSU ITMO contest. Petrozavodsk training camp. Winter 2008. Tags: graph theory |
