| ENG RUS | Timus Online Judge |
1606. SlalomTime limit: 1.0 second Memory limit: 64 MB Each weekend Petr goes mountain skiing with his friends. He has learned
recently that Winter Olympic Games will be held in his city in several years'
time. Now Petr dreams of winning a gold Olympic medal in slalom. In this
sport, a sportsman must go downhill performing sharp turns, and he mustn't miss
the gates placed on the mountain slope. 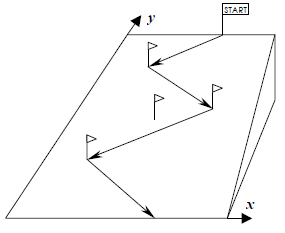 Petr started training at once because it was not much time left until the Games.
He created a training piste for himself by placing n poles on a slope.
Then he decided to calculate his downhill trajectory. For this, he plotted the
slope in the coordinate system shown in the picture. Petr can begin his
descent at any point on the start line (in the scheme, it is the line
y = 100000) and end it at any point of the finish line
(the line y = 0). His trajectory must be a broken line
with vertices at poles. The y coordinate must be decreasing at each moment.
Petr wants to ski downhill touching as many poles as possible and changing his
direction every time he touches a pole (i.e., if was going rightwards, he
must start going leftwards). He also may go through a pole in a straight line
without touching it. A possible trajectory is shown in the picture.
Calculate an optimal trajectory for Petr.
InputThe first line contains the number of poles n (no more than 50000).
The following n lines contain coordinates of poles in the form of
pairs of integers (xi, yi) separated
with a space; OutputIn the first line, output the maximal number of poles that Petr can touch when
he skis down the slope. In the second line, give the numbers of the poles in
the order of touching.
Samples
Problem Author: Alexander Toropov (prepared by Alexander Ipatov) Problem Source: IX USU Open Personal Contest (March 1, 2008) Tags: none |
