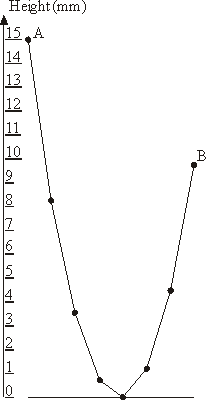The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.

The leftmost lamp is hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the i^th lamp height in millimeters as H_i we derive the following equations:

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75.

The input consists of a single line with two numbers N and A separated by a space. N (3 ≤ N ≤ 1000) is an integer representing the number of lamps in the garland, A is a real number representing the height of the leftmost lamp above the ground in millimeters (10 ≤ A ≤ 1000).

Output the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.