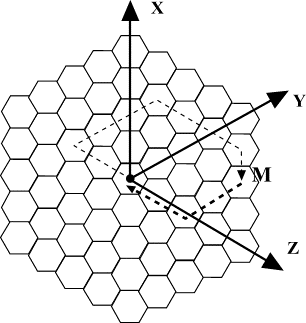Была предпринята попытка сосчитать все клюквины в болотах, расположенных вокруг Рыбинска. Оказалось, что удобно разделять поверхность болота на клетки, являющиеся правильными шести­угольниками. Одна из таких клеток — над которой завис вертолёт — назначена центральной. Были отмечены три направления (см. рисунок).

Нанятый студент приземлился в центральной клетке и бродил по болоту некоторое время. Он считал ягоды и по ходу движения записывал свои перемещения. Перемещения были записаны как последовательность переходов из одной клетки в другую через их общую сторону вдоль одного из отмеченных (или обратных им) направлений. Маршрут состоял из линейных отрезков, каждый из которых определялся направлением (X, Y или Z) и длиной (целое число со знаком, отличное от нуля). Движение в отмеченных направлениях представлялось положительными числами, в обратном направлении — отрицательными.

Ваша задача — написать программу, которая найдёт маршрут, состоящий из минимального количества клеток, из последней клетки, посещённой студентом, обратно в центральную клетку.

Первая строка ввода содержит n — длину маршрута (n > 0). Каждая из следующих n строк содержит букву, обозначающую направление (X, Y или Z), и число со знаком l (l ≠ 0), обозначающее длину отрезка в клетках. Буква и число разделены одним пробелом.

Студент отошёл от центральной клетки не более чем на 100 клеток в каждом из отмеченных или обратных направлений. Общая длина маршрута не превосходит 32 000 линейных отрезков.

Вывод должен содержать описание маршрута от последней клетки, посещённой студентом, до центральной клетки. Маршрут должен состоять из минимального количества клеток.

Первая строка вывода должна содержать m — количество отрезков в обратном маршруте, m ≥ 0. Следующие m строк вывода должны содержать описание отрезков обратного маршрута в том же формате, что и во вводе.