| ENG RUS | Timus Online Judge |
NEERC 2008, Четвертьфинал Восточного подрегиона
Соревнование завершено
C. Кратчайшая подцепьОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ 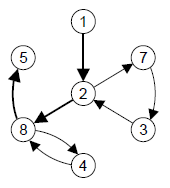 В ориентированном графе без кратных ребер и петель задана цепь p.
Требуется построить ее подцепь q, такую что:
Исходные данныеЦепь p задана списком вершин.
В первой строке записано целое число n — количество вершин в
списке (таким образом, цепь имеет длину РезультатВыведите номера вершин цепи q через пробел.
Цепь q может состоять из одной вершины.
Пример
Автор задачи: Владимир Яковлев (идея — Магаз Асанов) Источник задачи: NEERC 2008, Четвертьфинал Восточного подрегиона |
