Дерево Штерна-Броко — это изящная конструкция, позволяющая построить множество всех неотрицательных дробей. Строится она с помощью бесконечного последовательного выполнения одной итерации. Пусть на нулевой итерации у нас будет массив из двух дробей:

(вторая величина, строго говоря, дробью не является; её можно понимать как несократимую дробь, обозначающую бесконечность).

Дальше на каждой следующей итерации берутся две соседние дроби ^a/_b и ^c/_d и вставляется между ними их медианта, то есть дробь ^a+c/_b+d. Таким образом, на следующих итерациях получатся массивы:

Можно показать, что любое число, представимое в виде неотрицательной дроби, рано или поздно появится в этом массиве. А также никакая дробь не окажется в нём дважды. Давайте тогда для каждого числа запомним итерацию, после которой оно впервые появилось. Получается, после первой итерации появилась дробь ¹/₁, после второй — дроби ¹/₂ и ²/₁, и так далее.

Осталось только привести определение самого дерева Штерна-Броко. В корне этого бесконечного дерева находится дробь ¹/₁, а слева и справа от дерева находятся дроби ⁰/₁ и ¹/₀. Любая вершина дерева имеет двух сыновей, каждый из которых получается как медианта своего левого предка и правого предка. Получается, на глубине i этого дерева будут все те дроби, которые появились на i-й итерации: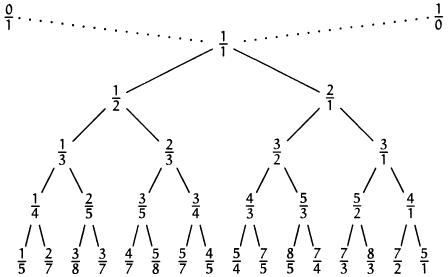

У этого дерева есть множество замечательных свойств, но они нас сегодня не интересуют. Задача состоит в том, чтобы найти дробь, которая находится на глубине N и является M-й по счёту слева.

В единственной строке даны два целых числа N и M — глубина и порядок слева необходимой дроби (1 ≤ N ≤ 10⁹, 1 ≤ M ≤ min(2^N−1, 10⁹)).

Выведите числитель и знаменатель этой дроби через пробел.