| ENG RUS | Timus Online Judge |
2200. Он вам не конь 2Ограничение времени: 4.0 секунды Ограничение памяти: 256 МБ Игорь — игрок в шахматы. После очередной тренировки Игорь со своим напарником решил сыграть, имея только одного коня, но с использованием не одной шахматной доски, а сразу нескольких. Напомним, что конь ходит буквой «Г» во всех направлениях так, что сначала двигается на 2 клетки по одной оси и на 1 — по другой. Все варианты одного хода для шахматного коня изображены на рисунке: 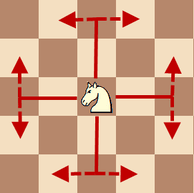 На прямоугольном столе, размеченном квадратной сеткой, Игорь разложил N досок, каждая из которых — прямоугольник размером не менее чем 3 × 3 (не менее 3 клеток по каждой из осей). Доски расположены так, что их стороны параллельны сторонам стола, а углы доски — строго в узлах квадратной сетки. Кроме того, никакие две доски не касаются друг друга ни сторонами, ни даже углами. В центре стола выбрано начало координат, сами координаты по модулю не превосходят M. В некоторую клетку одной из этих N досок Игорь поставил коня. Вам необходимо посчитать, сколько досок может посетить конь, последовательно совершая свои ходы. При этом ходить можно только по одной доске, а также между ними, если это можно сделать за один ход. Разрешается посещать ранее пройденные клетки и доски. Исходные данныеВ первой строке через пробел даны два целых числа N и M (1 ≤ N ≤ 5 · 104, 2 ≤ M ≤ 109). Во второй строке через пробел даны два целых числа x и y — координаты левого нижнего угла клетки, в которой находится конь (−M ≤ x, y < M). В каждой из следующих N строк через пробел даны по 4 целых числа: xLi, yLi, xRi, yRi, задающие очередную шахматную доску, где (xLi; yLi) — это координаты левого нижнего угла доски, а (xRi; yRi) — правого верхнего (−M ≤ xLi < xRi ≤ M, −M ≤ yLi < yRi ≤ M). Гарантируется, что размер доски по каждому из измерений не меньше 3, то есть xRi − xLi ≥ 3 и yRi − yLi ≥ 3, и что никакие две доски не касаются друг друга ни сторонами, ни даже углами. Гарантируется, что клетка с конём будет находиться на некоторой доске, то есть для некоторого i выполняется xLi ≤ x < xRi и yLi ≤ y < yRi. РезультатВ единственной строке выведите одно целое число — количество досок, которые может посетить конь, включая доску, с которой он начинает своё путешествие. Примеры
ЗамечанияИллюстрация к первому примеру: 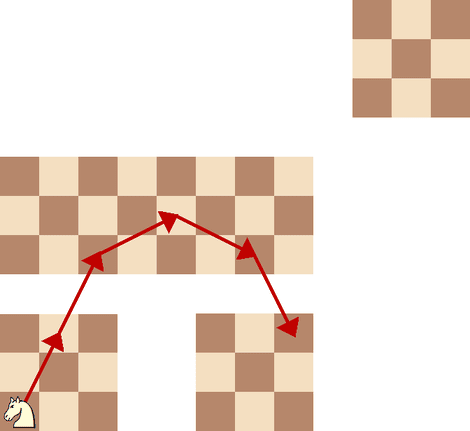 Автор задачи: Вадим Баринов Источник задачи: Вузовско-академическая олимпиада по информатике 2020 Метки: графы |
