| ENG RUS | Timus Online Judge |
2166. Две дорогиОграничение времени: 3.0 секунды Ограничение памяти: 256 МБ Очень многие слышали про Яндекс.Go, но немногие знают про новую секретную разработку Яндекс.GoRod, которая будет помогать при построении новых городов. Приложение будет представлять будущий город в виде плоскости с декартовыми координатами. На данном этапе уже проложены N железных дорог в виде бесконечных прямых, на каждом пересечении которых будет находиться станция. Для удобства работы с приложением, центр города располагается в центре координат, а дороги можно прокладывать только параллельно осям координат. Само собой, нужно соединить центр города с каждой из запланированных станций. Легко догадаться, что для этого потребуются не больше чем две дороги: горизонтальная и вертикальная. Но вот труднее понять то, сколько придётся потратить денег на это. Известно, что один километр дороги стоит один миллион рублей. Для начала решили соединить центр города с самой дорогой по стоимости прокладывания дорог станцией. Помогите разработчикам приложения Яндекс.GoRod реализовать функцию, позволяющую найти эту стоимость. Исходные данныеВ первой строке дано целое число N — количество железных дорог (2 ≤ N ≤ 105). В следующих N строках описаны эти железные дороги четырьмя целыми числами x1i, y1i, x2i, y2i — координаты двух различных точек, через которые проходит прямая, содержащая железную дорогу. Все координаты даны в километрах и по модулю не превосходят 1000. Гарантируется, что в вводе нет параллельных прямых. РезультатВыведите наибольшую стоимость соединения центра города со станцией не более чем двумя дорогами, параллельными осям координат, в миллионах рублей. Ответ будет засчитан, если абсолютная или относительная погрешность значений не превосходит 10−4. Формально, пусть ваш ответ равен x, а ответ жюри равен y. Ваш ответ считается правильным, если |x−y| / max(1,|y|) ≤ 10−4. Пример
ЗамечанияИллюстрация к примеру (первая, вторая и третья дороги обозначены a, b и c соответственно):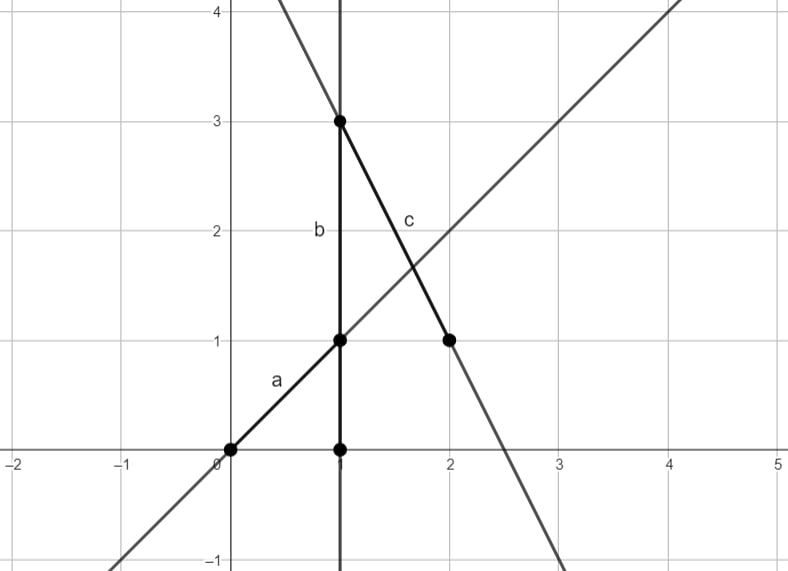 Автор задачи: Вадим Баринов Источник задачи: Уральская командная олимпиада по программированию 2022 Метки: геометрия |
