| ENG RUS | Timus Online Judge |
2076. ВасианаОграничение времени: 2.0 секунды Ограничение памяти: 256 МБ Вася изобразил на координатной плоскости множество точек
(x0, y0) таких, что существует хотя бы одно действительное значение параметра t,
при котором a · t2 + b · t + c = x0 и d · t2 + e · t + f = y0.
Получилась интересная кривая — у неё была ось симметрии, и
возможно, что и не одна! Вася понял, что сделал математическое открытие, и
решил назвать нарисованную кривую васианой. Исследуя математические свойства васианы, Вася отметил на плоскости точку
P = (Px, Py), выбрал одну из осей симметрии васианы и провёл
перпендикуляр к ней из точки P. Основание этого перпендикуляра он
обозначил точкой Q. Верно ли, что круг с центром в точке Q радиуса R имеет общие точки с
васианой? 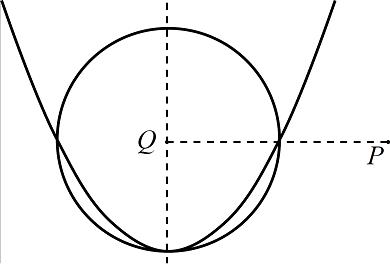 Исходные данныеВходные данные состоят из нескольких тестов. В первой строке записано
целое число T — количество тестов (1 ≤ T ≤ 7000).
Далее следуют T блоков по три строки каждый, содержащие тесты. Блок имеет следующий формат: a b c d e f Px Py R Все числа в блоке целые и по модулю не превосходят 1020. R ≥ 1. РезультатЕсли круг и васиана гарантированно имеют общие точки, выведите «YES».
Если круг и васиана гарантированно не имеют общих точек, выведите «NO».
Если это зависит от того, какая ось симметрии васианы была выбрана,
выведите «MAYBE».
Гарантируется, что васиана имеет хотя бы одну ось симметрии. Пример
ЗамечанияКругом радиуса R с центром в точке P называется множество точек, каждая точка которого находится на расстоянии не больше R от P. Васиана в примере — это парабола y = x2. Она имеет единственную ось
симметрии x = 0. На рисунке видно, что часть этой параболы лежит внутри
круга с центром в Q = (0, 1) радиусом 1. Автор задачи: Михаил Рубинчик Метки: геометрия сложнейшая задача |
