| ENG RUS | Timus Online Judge |
2069. Тяжёлый рокОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Илья — лидер самой популярной хард-рок группы на Земле. И к выходу нового сингла группа решила записать самый крутой клип из когда-либо созданных: Илья проедет по Манхэттену, стоя на крыше огромного грузовика и играя потрясающие воображение соло-партии. А в это время восторженные жители острова будут подпевать и качать головой в ритм песни. Есть только одна проблема: далеко не на всех улицах любят рок... Напомним, что Манхэттен состоит из n вертикальных и m горизонтальных улиц, образующих сетку из (n − 1)×(m − 1) кварталов.
Продюсер Ильи провёл исследование и выяснил, что популярность группы, во-первых, постоянна на протяжении всей улицы, и, во-вторых, её можно задать целым числом от 1 до 109. Так, если рокеры проедут по улице, где их популярность равна 109, то их встретят градом оваций, салютом, лазерным шоу и ящиками... предположим, апельсинового сока. Однако если они проедут по улице, где их популярность равняется 1, они немедленно будут закиданы помидорами и тухлыми яйцами. Что, разумеется, не пойдёт на пользу крутости клипа! Итак, по задумке маршрут должен проходить из самого верхнего левого перекрёстка в самый нижний правый. Определим крутость маршрута как минимальную популярность группы среди всех улиц, по которым рокеры проедут ненулевое расстояние. Как вы уже, наверное, догадались, музыканты хотят найти маршрут с самой большой крутостью. Если поможете им, Илья даже даст вам свой автограф! Исходные данныеВ первой строке через пробел даны целые числа n и m (2 ≤ n, m ≤ 105) — количества вертикальных и горизонтальных улиц соответственно. В следующих n строках по одному в строке даны значения популярности группы на вертикальных улицах в порядке слева направо. В следующих m строках по одному в строке даны значения популярности группы на горизонтальных улицах в порядке сверху вниз. Гарантируется, что все значения популярности группы — целые числа от 1 до 109. РезультатВыведите целое число — максимально возможную крутость маршрута. Примеры
ЗамечанияПояснение к первому примеру (выделен самый «крутой» маршрут): 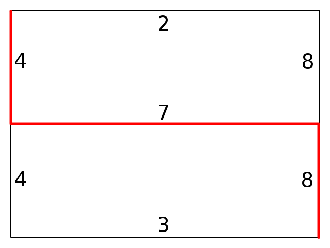 Автор задачи: Олег Меркурьев (подготовка — Александр Борзунов) Источник задачи: Уральская региональная командная олимпиада по программированию 2015 Метки: нет |
