| ENG RUS | Timus Online Judge |
2019. Пара: нормальное и паранормальноеОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Если вы окажетесь на заброшенном ядерном полигоне в Неваде во время
Хэллоуина, то станете свидетелем весьма необычного зрелища. Каждый год
охотники за привидениями проводят здесь испытание новых модификаций своего
протонного бластера. На полуокружности размещаются n охотников и n ловушек
с привидениями. В каждой ловушке находится ровно одно привидение.
Привидения в ловушках могут быть разных видов, а оружие в
руках каждого охотника способно нейтрализовать только один вид
потусторонней нечисти. На счёт три все ловушки разом открываются, и все охотники
открывают огонь. Естественно, каждый охотник выбирает в качестве цели то
привидение, которое сможет нейтрализовать его бластер. И самое главное —
протонные лучи бластеров не должны пересекаться! 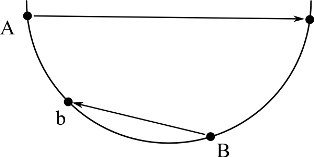 Перед вами схема расположения охотников и ловушек на предстоящем в этом
году испытании. Определите для каждого охотника, в какое привидение он
должен стрелять, чтобы все привидения были нейтрализованы и никакие два
луча не пересеклись. Считайте, что лучи всех бластеров лежат в одной
горизонтальной плоскости и не пробивают привидения насквозь, попадая в них. Исходные данныеВ первой строке записано целое число n — количество охотников
(1 ≤ n ≤ 5 000). Во второй строке записана последовательность из
2n латинских букв, описывающая расположение охотников
и ловушек на полуокружности. Заглавные буквы соответствуют охотникам, а
строчные — ловушкам. Например, буква «a» обозначает ловушку с
привидением вида «a», а буква «A» — охотника c бластером,
способным нейтрализовать привидения вида «a». В последовательности ровно
n строчных букв и ровно n заглавных букв. РезультатЕсли задача имеет решение, выведите через пробел целые числа g1, g2,
…, gn, где gi — номер привидения, в которое должен стрелять i-й
охотник. И охотники, и привидения нумеруются целыми числами от 1 до n в
порядке их расположения на полуокружности. Все gi должны быть попарно
различными. Если задача имеет различные решения, выведите любое из них.
Если задача не имеет решения, выведите «Impossible». Примеры
Автор задачи: Денис Дублённых (подготовка — Олег Меркурьев) Источник задачи: NEERC 2014, Четвертьфинал Восточного подрегиона Метки: нет |
