| ENG RUS | Timus Online Judge |
1963. Воздушный змейОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Вова купил себе на рынке в Гуанчжоу набор для изготовления воздушного змея.
На следующий день выдалась хорошая погода, и он решил склеить змея и
запустить его. Инструкция по изготовлению, конечно, была только на
китайском языке, поэтому Вова решил, что разберётся и без неё. Немного
повозившись, он соорудил змея в форме плоского четырёхугольника,
оставалось только приклеить к нему хвост. И тут Вове пришлось задуматься над тем, к какой точке границы
четырёхугольника должен быть приклеен хвост змея. Интуиция подсказала
ему, что для того, чтобы полёт змея был устойчивым, его хвост должен
лежать на некоторой оси симметрии четырёхугольника. На двух рисунках слева
изображены воздушные змеи, летающие устойчиво, а на двух рисунках справа —
змеи, летающие неустойчиво. 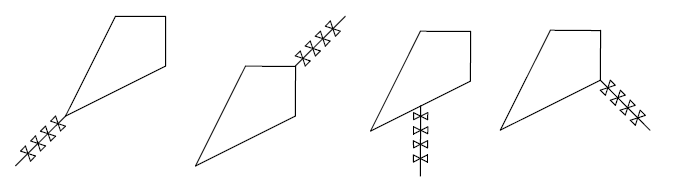 Сколько существует точек на границе четырёхугольника, таких что, если
приклеить к ним хвост, в результате получится воздушный змей, летающий
устойчиво? Исходные данныеВ четырёх строках записаны координаты вершин четырёхугольника в порядке
обхода. Все координаты — целые числа, по модулю не превышающие 1 000.
Никакие три последовательные вершины четырёхугольника не лежат на одной прямой.
Противоположные стороны четырёхугольника не пересекаются. РезультатВыведите количество точек на границе четырёхугольника, к которым можно
приклеить хвост змея. Примеры
ЗамечанияОсью симметрии плоской фигуры называется прямая, лежащая в плоскости фигуры и такая, что при отражении относительно неё фигура переходит сама в себя.
Автор задачи: Александр Ипатов Источник задачи: Открытое личное первенство УрФУ по программированию 2013 Метки: геометрия |
