| ENG RUS | Timus Online Judge |
1845. Целочисленный комплексный определительОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Целым Гауссовым числом называется комплексное число с целочисленными составляющими.
Если a, b, q, r — целые Гауссовы числа, a = bq + r, |r| < |b|, то r называется остатком от деления a на b. Дано целое Гауссово число p и матрица X = (xij) размером n × n, элементы которой также являются целыми Гауссовыми числами. Посчитайте остаток от деления определителя матрицы X на p. Напомним, что определитель матрицы X равен 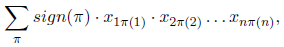 где сумма берётся по всему множеству перестановок n элементов.
Сложение и умножение являются обычными сложением и умножением комплексных чисел. Исходные данныеВ первой строке записано целое число n (1 ≤ n ≤ 50). В каждой из следующих n строк через пробел записаны
n комплексных чисел — элементы матрицы X. В последней строке записано комплексное число p, не равное нулю.
Комплексное число задаётся действительной и мнимой частью, записанными через пробел.
Все составляющие комплексных чисел не превосходят по модулю 10 000. РезультатВыведите через пробел действительную и мнимую часть остатка от деления определителя X на p.
Если возможных ответов несколько, выведите любой. Гарантируется, что ответ существует. Пример
Автор задачи: Дмитрий Полетаев, Иван Бурмистров Источник задачи: Ural SU Contest. Petrozavodsk Summer Session, August 2010 Метки: нет |
