| ENG RUS | Timus Online Judge |
1814. Цепная дробьОграничение времени: 0.5 секунды Ограничение памяти: 64 МБ Известно, что любое иррациональное число d большее единицы можно
представить в виде бесконечной цепной дроби:
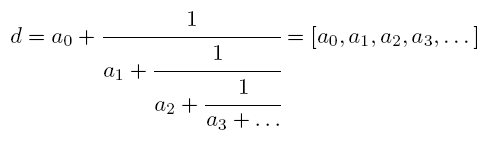 Здесь ai — это положительные целые числа. Подходящей цепной дробью порядка k для числа d называется рациональное число [a0, a1, …, ak], полученное рассмотрением первых k + 1 элементов цепной дроби для d.
Требуется по данному целому числу x вычислить числитель и знаменатель
подходящей цепной дроби порядка k для квадратного корня из x.
Исходные данныеВ единственной строке записаны целые числа x и k
(2 ≤ x ≤ 106; 0 ≤ k ≤ 109). Число x не является
полным квадратом.
РезультатВыведите значение подходящей цепной дроби порядка k для квадратного корня из x в виде несократимой дроби. Числитель и знаменатель требуется выводить по
модулю 109 + 7.
Пример
Источник задачи: Tavrida NU Akai Contest. Petrozavodsk Summer Session, August 2010 Метки: нет |
