| ENG RUS | Timus Online Judge |
1805. Чапаев и шифровальная решёткаОграничение времени: 0.5 секунды Ограничение памяти: 64 МБ Во время обыска в брошенном штабе белых Петька и Чапаев нашли квадраты
размером n × n, заполненные буквами. Чапаев предположил, что белые
вели секретную переписку с помощью шифровальной решётки, а
квадраты — это зашифрованные сообщения.
 Шифровальная решётка — бумажный квадрат размером n × n
клеток, в котором вырезаны n2/4 клеток-окошек. Наложив решётку на
листок бумаги, имеющий такой же размер, её обладатель пишет в окошках
первые n2/4 символов сообщения. После этого он поворачивает решётку
по часовой стрелке на 90 градусов. Он записывает в окошках следующие
n2/4 символов сообщения, после чего вновь поворачивает решётку на 90
градусов. Записав очередные n2/4 символов, он делает ещё один поворот
решётки и после этого пишет последние n2/4 символов сообщения.
Шифровальная решётка устроена так, что после каждого поворота она
закрывает все уже написанные символы, а в окошках открываются чистые
клетки.
Несмотря на долгие поиски, ни одной шифровальной решётки так и не было
обнаружено. Очевидно, белые уничтожили их, когда оставляли штаб.
На следующий день Анка заметила, что на
стене штаба написано целое число k. Она тут же сообщила об этом Чапаеву,
который сообразил, что белые пользовались k-й в лексикографическом
порядке шифровальной решёткой. Выходит, для того чтобы прочитать
зашифрованные сообщения белых, Чапаеву нужно лишь
изготовить такую же решётку.
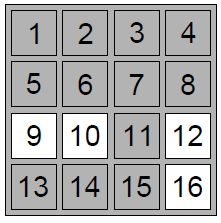
Все шифровальные решётки можно закодировать матрицами из нулей и единиц
размером n × n так, чтобы клетки-окошки обозначались единицами,
а все остальные клетки — нулями. Будем говорить, что матрица a
лексикографически меньше матрицы b (обе матрицы имеют размер n × n),
если существует такое число i, что первые i клеток матриц a
и b совпадают, в (i+1)-й клетке матрицы a стоит ноль, а в (i+1)-й клетке
матрицы b — единица. Клетки матриц нумеруются как показано на рисунке.
Исходные данныеВ единственной строке записаны целые числа n и k (4 ≤ n ≤ 10;
n чётно; 1 ≤ k ≤ 1018). Гарантируется, что число k не
превосходит общего количества шифровальных решёток размером n × n.
РезультатВыведите решётку, которую должен изготовить Чапаев, чтобы прочитать
сообщения белых.
Пример
Автор задачи: Александр Ипатов Источник задачи: NEERC 2010, Четвертьфинал Восточного подрегиона Метки: нет |
