| ENG RUS | Timus Online Judge |
1606. СлаломОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Юный Петя каждые выходные ездит с друзьями кататься на горных лыжах.
Недавно он узнал, что через несколько лет в его городе пройдут зимние Олимпийские игры,
и теперь мечтает завоевать на них золотую медаль в слаломе.
В этом виде спорта при спуске с горы участник соревнований должен делать
резкие повороты, причём ему нельзя пропускать ни одной пары ворот,
расставленных на трассе. 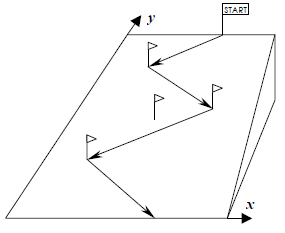 Петя немедленно приступил к тренировкам, ведь до олимпиады осталось не так
уж много времени. Сначала он устроил себе тренировочную трассу, поставив
на склоне горы n флажков, а затем решил рассчитать траекторию спуска.
Для этого он начертил схему склона в системе координат, изображённой на рисунке.
Петя может начинать спуск в любой точке линии старта (на схеме это прямая
y = 100000) и заканчивать его в любой точке линии финиша
(прямая y = 0). Он должен постоянно двигаться по
траектории, которая имеет вид ломаной с вершинами в точках-флажках, в
направлении уменьшения координаты y.
Петя поставил перед собой задачу спуститься с горы, коснувшись наибольшего
количества флажков и меняя направление спуска при касании каждого флажка
(т.е. он должен начать двигаться направо, если до этого двигался налево, и
наоборот). У него есть возможность проехать через флажок по прямой, не
касаясь его.
Возможный вид траектории движения Пети представлен на рисунке. Определите, каких флажков, и в каком порядке должен коснуться Петя. Исходные данныеВ первой строке дано целое положительное число n — количество флажков
(не более 50000). Далее в n строках перечислены координаты флажков
в виде пар целых чисел (xi, yi), разделённых пробелом
РезультатВ первой строке выведите максимальное количество флажков, которых
может коснуться Петя при спуске. Во второй строке выведите через пробел
номера этих флажков в порядке касания. Примеры
Автор задачи: Александр Торопов (подготовка — Александр Ипатов) Источник задачи: Девятое открытое личное первенство УрГУ (1 марта 2008) Метки: нет |
