| ENG RUS | Timus Online Judge |
1360. Философский спорОграничение времени: 2.0 секунды Ограничение памяти: 64 МБ На одном банкете сошлись как-то в жарком споре математик и философ.
Философ говорит: — Идеальная линия — это длина без толщины, поэтому у линии не может быть площади. А математик в ответ: — Так-то оно так, однако ж можно одной линией квадрат так закрасить, что ни одной щёлочки не останется, а площадь у квадрата точно есть, — а сам про себя ехидно улыбается. Не поверил философ: — Покажи, — говорит, — мне эту линию. — Да пожалуйста… — говорит математик и пишет на бумажке: 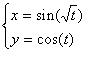 — Если t будет расти, то точка (x, y) будет по квадрату бегать, линию рисовать. — И что? — говорит философ. — Как это она закрасит весь квадрат? — А так, — отвечает математик, — какую точку в квадрате не нарисуй, она когда-нибудь очень близко от неё пройдёт. — Нет, — говорит философ, — всё равно не верю. Вот когда она через вот эту точку пройдёт? — и он поставил в квадрате жирную точку. Ответьте что-нибудь философу. Исходные данныеВ первой строке находятся координаты точки (x0, y0) (−1 ≤ x0, y0 ≤ 1).
Во второй строке находится ε ≥ 0.0001 — радиус нарисованной точки (жирная точка — это маленький кружок). РезультатЛюбое значение t в пределах [0,1012], при котором кривая пересечёт нарисованную "точку", или слово "FAIL", если кривая не проходит достаточно близко от указанной точки. Пример
Автор задачи: Станислав Васильев (идея — Ден Расковалов) Источник задачи: IX Чемпионат Урала по спортивному программированию. Екатеринбург, УрГУ, 19-24 апреля 2005 г. Метки: математика |
