| ENG RUS | Timus Online Judge |
1138. Целочисленные процентыОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Поступая на новую работу, программист Н. Смарт требовал, чтобы его новая зарплата (в рублях, положительное целое число) была больше его предыдущей зарплаты на целое число процентов. Каким может быть максимальное количество работ, которые сменил мистер Смарт, если его последняя зарплата не превышала n, а его первая зарплата была ровно s рублей? Пример. Пусть n = 10, s = 2, тогда m = 5. Последовательность 2, 4 (+100%), 5 (+25%), 8 (+60%), 10 (+25%) — самая длинная, хотя и не единственная, из последовательностей, удовлетворяющих условию задачи. Значения процента увеличения зарплаты указаны в скобках. 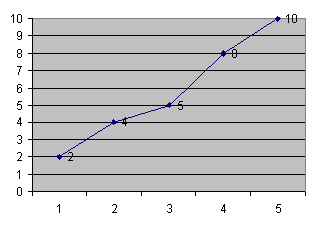 Исходные данныеДва целых числа n и s, разделённые пробелами. 1 ≤ n, s ≤ 10 000. РезультатОдно целое число m — максимальное количество предыдущих работ Н. Смарта. Пример
ЗамечанияВ случае n = s ответ равен 1. Источник задачи: Четвертьфинал, центральный регион России, Рыбинск, 17–18 октября 2001 Метки: нет |
