| ENG RUS | Timus Online Judge |
1024. ПерестановкиОграничение времени: 2.0 секунды Ограничение памяти: 64 МБ ВступлениеНапомним, что перестановкой на некотором конечном множестве называется взаимно однозначное отображение этого множества на себя. Менее формально, перестановка — это способ переупорядочить элементы множества. Например, на множестве {1, 2, 3, 4, 5} можно задать перестановку 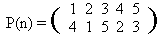 Такая запись определяет перестановку P следующим образом: P(1)=4, P(2)=1, P(3)=5 и т.д. А чему равно значение выражения P(P(1))? Совершенно понятно — P(P(1))=P(4)=2. А, например, P(P(3))=P(5)=3. Легко понять, что если P(n) — перестановка, то и P(P(n)) тоже перестановка. В нашем примере (проверьте!) 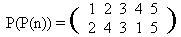 Естественно тогда обозначить эту перестановку так: P(P(n))=P2(n). Более общее определение выглядит так: P(n)=P1(n), Pk(n)=P(Pk-1(n)). Среди всех перестановок особое положение занимает одна — та, которая ничего не переставляет: 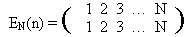 Совершенно понятно, что для любого k верно соотношение (EN)k=EN. Справедливо и менее тривиальное утверждение (мы не будем здесь его доказывать; решая задачу вы сами попутно получите доказательство): Пусть P(n) — некоторая перестановка множества из N элементов. Тогда существует такое целое положительное число k, что Pk=EN. Наименьшее целое положительное k, такое, что Pk = EN, называется порядком перестановки P. ЗадачаЗадача, которую должна решать программа, формулируется теперь очень просто: «дана перестановка, найти ее порядок». Исходные данныеВ первой строке записано единственное целое число N, удовлетворяющее двойному неравенству РезультатВыведите порядок перестановки P. Можно считать, что ответ всегда не превосходит 109. Пример
Автор задачи: Никита Шамгунов Источник задачи: Второе командное соревнование школьников Свердловской области по программированию, 7 октября 2000 Метки: математика |
