| ENG RUS | Timus Online Judge |
NEERC, Центральный подрегион, Рыбинск, октябрь 2001
Соревнование завершено
A. Последовательность ФибоначчиОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ 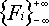 — бесконечная последовательность целых чисел, удовлетворяющая условию Фибоначчи Fi + 2 = Fi + 1 + Fi для любого целого i. Напишите программу, которая вычисляет значение Fn по заданным значениям Fi и Fj. Исходные данныеВвод содержит пять целых чисел в следующем порядке: i, Fi, j, Fj, n. −1000 ≤ i, j, n ≤ 1000, i ≠ j, −2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)). РезультатВывод состоит из одного целого числа — значения Fn. Пример
ЗамечанияВ примере дано: F3 = 5, F−1 = 4; требуется найти значение F5. По известным значениям восстанавливается следующая последовательность Фибоначчи: …, F−1 = 4, F0 = −1, F1 = 3, F2 = 2, F3 = 5, F4 = 7, F5 = 12, … Таким образом, ответ: F5 = 12. Источник задачи: Четвертьфинал, центральный регион России, Рыбинск, 17–18 октября 2001 |
