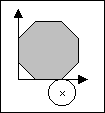In the problem you are to determine the minimal diameter that may compensate inexactness of projectile hit in each concrete case. Assume that all the targets are convex polygons. A hit is the situation when the circle crater that the projectile leaves (the crater diameter equals to the one of the projectile) covers at least one point of the target.

The first line contains three numbers — coordinates of the hit point of the projectile center and the number of polygon sides N (3 ≤ N ≤ 100). The next N lines contain the vertices coordinates in counter-clockwise order. All the coordinates are integers from [−2000,2000].

You are to output the only number which is the minimal diameter of a projectile that will cover the target rounded with three digits after the decimal point.