| ENG RUS | Timus Online Judge |
Ural Championship 2005 Round I
Contest is over
G. Dean's Pyramid 2Time limit: 2.5 second Memory limit: 64 MB At Ural Championship 2004 there was a task "Dean's pyramid". Briefly it looks like the following:
There is an egiptian like glass pyramid on the table of Ural State University mathematics and mechanics faculty dean. The faculty legend says that before weak student gets sent down, dean gives the student the last chance. He puts unsigned list of dismissed students at one side of the table, and puts the pyramid at another side. If the student is able to move the pyramid to the locus of deans signature on the dismissing listplace, by rolling the pyramid over the edges for no more than 70 times, the student stays at the faculty (for the last time). The task was to determine, how close the pyramid can be moved to the target point under the following conditions. The pyramids base is square and its lateral faces are regular triangles. You can roll the pyramid by turning it from one face to the adjacent one over some edge. During this turning the edge should not slide on surface of the table. If after the turn over some edge the pyramid stands on its base, the next turn can be performed either over the same edge or over the opposite edge of the pyramids base only. There are no restrictions on the rolling from the triangle faces. After Ural Championship 2004 weak students felt secured: now they know the secrets of dean's pyramid and the simplest algorithm to find the points on the table where the pyramid could be. To learn this algorithm is much, much simpler than to learn theorems. And you never get sent down! The only doubt disturbed them: what if authors of the task garbled something... And they were right: looking at the hidden camera picture it was found that side faces of the pyramid were not regular triangles, but only isosceles one! And strange rule of rolling the pyramid could be just a fiction of task authors... Weak students feel distress again... You see, this could be a legend. And could be a truth. The pyramid is so real, and it looks so beautiful at the dean's table...
So help the students for the last time. Try to determine the best way of rolling the pyramid to put it as close as possible to the point of dean's signature.
You are given a number N — the maximum number of rolls allowed by the dean. You are also given an exact size of the pyramid: the length of an edge of square face A1 and the length of a side edge A2. Both lengths are given in centimetres. It was estimated by eye that a value of A2/A1 is in a range from 0.9 to 1.9. It is known that the dean is severe enough, so he puts dismissing list far enough from the pyramid. You may assume that the pyramid is originally
placed not closer than 20.05 * A1 to the point of the dean's signature. Pyramid originally stands on its base with
a center of the base placed at the point (0,0) and with edges of the base parallel to the axes of coordinate system. You are to find the sequence of rolls by which the pyramid gets to the point (X,Y) as close as possible. After the last roll the pyramid
again must stand on its base, though edges of the base could be arbitrary oriented.
But the distance between the center of the pyramid base and the point (X,Y) must be as small as possible. In the case of tie, you also have to minimize the number of rolls. You are allowed to make less than N rolls.
The pyramid can be rolled from one face to another only via their common edge. And the edge should not slide on surface of the table during the roll. InputInput contains the numbers A1 and A2
(in centimetres, both in range from 0.1 to 10). Two numbers X and Y follows. They are the coordinates of sacramental point of the dean's signature. The number N (2 ≤ N ≤ 32) ends the input. OutputYou have to conform the following format. First of all pring the distance between the center of the pyramid base and the signature point in the pyramid's final placement. This distance must be printed correct to three places of decimals. Then print the number M (0 ≤ M ≤ N) of rolls required to get the printed distance. 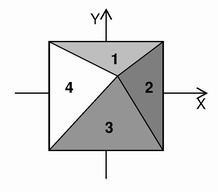 Then print M+1 numbers — the numbers of the faces on which the pyramid stands after each roll. Separate these numbers with spaces. And do not forget to start this list with the number of the pyramid base on which it stands initially. Faces of the pyramid are numbered according to the following scheme. The pyramid's base has number 0. The side faces are numbered clockwise by 1, 2, 3 and 4 being looked
from the top of the pyramid standing on it's base. The face of the pyramid which looks to positive direction of 0Y axis has a number 1.
Sample
Problem Author: Aleksandr Mironenko Problem Source: IX Urals Programming Contest. Yekaterinburg, April 19-24, 2005 |
