| ENG RUS | Timus Online Judge |
NEERC 2008, Eastern subregion quarterfinals
Contest is over
E. Death ConveyorTime limit: 1.0 second Memory limit: 64 MB 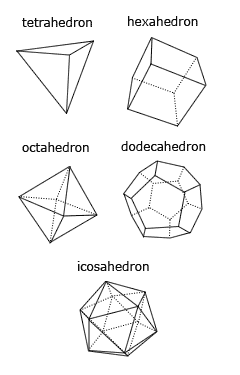 The Empire experienced a severe economic crisis. Enormous funds had been spent on
constructing Death Stars, but the Rebels had easily destroyed every single one of them.
In this situation, there were two possible courses of action: either start peace
negotiations with the Rebels and try to find a political solution to the
conflict (and Darth Vader was definitely against that), or substantially cheapen
the cost of constructing Death Stars. The second variant was chosen.
The production was transferred to a neighboring galaxy, where labor was
much cheaper. The industry there had long ago mastered the output of gigantic steel
beams with a length of 1 standard sidereal unit. The assemblage of Death Stars
from such beams was started. The Death Stars had the form of regular
polyhedra (Platonic solids). At each vertex of such a polyhedron, a megagun was
mounted; it could shoot along the ray originating from the center of the polyhedron
and passing through that vertex. When the early-warning station detected an
approaching Rebel ship, the whole Death Star turned so that the nearest megagun
was aimed exactly at the ship. The amount of fuel consumed for the turning was
proportional to the angle of rotation. The shot inevitably destroyed the Rebel's
ship, and the Death Star remained in that position until the next attack.
In spite of the overwhelming technical advantage of the Empire, the Rebels
continued attacking Death Stars, and the Empire continued spending huge sums on
fuel and ammunition. The Imperial Minister of Finance was in despair. He
planned to raise the issue of peace negotiations once again at the Emperor's audience.
However, to protect himself from Darth Vader's anger, he wanted to present a
clear economic justification. That is why he asked you to calculate the amount
of fuel spent on repelling the Rebels' attacks.
InputThe first line specifies the Platonic solid in the form of which a Death Star is constructed. The names and main characteristics of these solids are given in the table below.
In the following line you are given the number n of the Rebels' attacks
repelled by this Death Star OutputOutput the cumulative angle of rotation in radians accurate to
five fractional digits.
Sample
Problem Author: Pavel Atnashev Problem Source: NEERC 2008, Eastern subregion quarterfinals |
