The Stern-Brocot tree is an elegant structure that allows the construction of the set of all non-negative fractions. It is built through an infinite sequence of iterations. At the zero iteration, we start with an array of two fractions:

(the second value, strictly speaking, is not a fraction; it can be understood as an irreducible fraction representing infinity).

Then, at each subsequent iteration, two adjacent fractions ^a/_b and ^c/_d are taken, and their mediant, that is, the fraction ^a+c/_b+d, is inserted between them. Thus, the arrays for the next iterations will be:

It can be shown that any number that can be represented as a non-negative fraction will eventually appear in this array. Also, no fraction will appear in it more than once. Therefore, for each number, we will remember the iteration after which it first appeared. Thus, after the first iteration, the fraction ¹/₁ appeared, after the second iteration — fractions ¹/₂ and ²/₁, and so on.

Now we just need to provide the definition of the Stern-Brocot tree itself. At the root of this infinite tree is the fraction ¹/₁, and to the left and right of the tree are the fractions ⁰/₁ and ¹/₀. Each vertex of the tree has two children, each of which is obtained as the mediant of its left ancestor and right ancestor. Thus, at depth i of this tree, there will be all those fractions that appeared at the i-th iteration: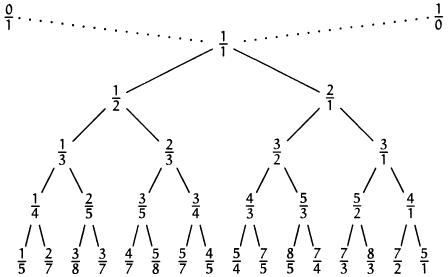

This tree has many remarkable properties, but they are not of interest to us today. The task is to find the fraction that is at depth N and is the M-th from the left.

The input consists of a single line containing two integers N and M — the depth and the order from the left of the required fraction (1 ≤ N ≤ 10⁹, 1 ≤ M ≤ min(2^N−1, 10⁹)).

Output the numerator and denominator of this fraction separated by a space.