| ENG RUS | Timus Online Judge |
1703. Robotic ArmTime limit: 1.0 second Memory limit: 64 MB 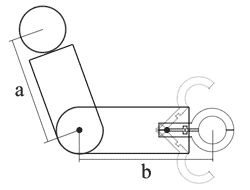 A robotic arm, like a human arm, consists of an upper arm and forearm.
The upper arm is attached to the shoulder joint and can rotate at the joint
in any direction. The forearm is attached to the upper arm at the elbow joint.
The forearm can turn with respect to the upper arm about the axis that passes
through the elbow joint and is perpendicular to both upper arm and forearm.
The angle at which the arm is bent at the elbow can't be acute. At the end of
the forearm there is a claw consisting of two equal parts. The claw can open
and close. When the claw is completely closed, it can hold a cylinder of a unit diameter.
In this position the axis of the cylinder is parallel to the axis of the elbow
joint.
There is a cylindrical rail of a unit diameter and infinite length near the robot.
The robot wants to grip the rail. The claw is now open and in the end it
must be completely closed around the rail. Determine the final position of the
robot's arm.
InputIn the first line you are given the length of the upper
arm a and the length of the forearm b. In the second and the third lines
there are the coordinates of two different points on the axis of the rail. The origin of the coordinate system is the shoulder joint. The rail does not pass through the shoulder. All the numbers are integer and their absolute values do not exceed 100; a, b ≥ 4. The thickness of the upper arm and forearm is negligible. OutputIf there is no position of the robotic arm in which the claw can be closed on
the rail, output “No solution.” Otherwise, output the coordinates
of the elbow joint and the angle at which the arm is bent in radians with the
maximal possible accuracy. The value of the angle must be in the range [π/2, π].
If there are several variants of the solution, output any one of them.
Samples
Problem Author: Pavel Atnashev Problem Source: The 13th Urals Collegiate Programing Championship, April 04, 2009 Tags: geometry |
