One day, mathematician and philosopher were engaged in a heated dispute.

Philosopher said:
— Ideal line has only length and no width, therefore, no line can have an area.
Mathematician replied:
— That's as it may be, but still you can fill a square with a line in such a way that there will be no gaps.
And you can't deny that a square has an area, and he grinned.
But Philosopher still wasn't convinced:
— Show me this line, then.
— With pleasure… — responded Mathematician and scribbled some equations on a piece of paper: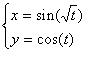

— With t increasing, the point (x, y) will move around the square, forming a line.
— So what? — asked Philosopher. How is it going to fill the entire square?
— Indeed, it will, — said Mathematician, — Whichever point inside the square you draw, the line will eventually cross that point.
— No, — replied Philosopher indignantly, — Anyway, I don't believe. When will the line cross this point? — and he put a thick dot inside the square.

Give Philosopher an answer.

The first line of input contains the coordinates (x₀, y₀) of the dot center (−1 ≤ x₀, y₀ ≤ 1). The second line contains ε ≥ 0.0001 — the radius of the dot (the dot is essentially a small circle).

Any value of t in the segment [0, 10¹²], which corresponds to the line crossing the dot, or "FAIL", if the line doesn't cross the dot.